OOF2: The Manual

Mechanical:Elasticity:Isotropic
	6.4.1. Material Properties

Name

Mechanical:Elasticity:Isotropic — Isotropic linear elasticity.

Details

Property Category: Elasticity
Parameters:

cijkl

Type: An object of the IsotropicRank4Tensor class.
Fields: Displacement
Fluxes: Stress

Discussion

The isotropic elasticity Property specifies that the Stress depends linearly and isotropically on the gradients of the Displacement, $u$ :

$\sigma_{ij} = C_{ijkl}\epsilon_{kl}$

(6.1)

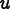where 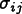$\sigma_{ij}$ is the Stress, 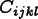$C_{ijkl}$ is an isotropic fourth rank tensor given by the modulus cijkl, and $\epsilon$ is the linear geometric strain,

$\epsilon_{ij} = \frac12\left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right).$

(6.2)

This form of the strain is not invariant under rigid rotations and is inappropriate for problems with large strains, which should use large strain elastic properties instead.


Color		Mechanical:Elasticity:Anisotropic:Cubic