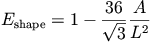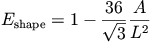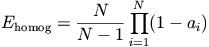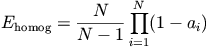OOF: Finite Element Analysis of Microstructures
| Submenus | Functions | Variables |
|---|---|---|
| groups | create | alpha_E=0.3 |
| materials | destroy | redraw=true |
| refine | anneal | |
| select | relax | |
| stack | smooth | |
| swap_two | ||
| swap_worst | ||
| E_range | ||
| save | ||
| sanity_check |
Adaptive meshing is one of the most powerful aspects of ppm2oof. The goal is to create a mesh of triangles each of which covers a homogeneous set of pixel properties and each of which is as equilateral as possible. [27]
Homogeneity is desired because you want the element to reflect the material properties that you have carefully selected and specified. Equilateral triangles are desired because they reduce the discretization error in the subsequent computation.
Homogeneity will be best achieved if the edges of all the triangles lie either on the interfaces between materials of differing properties, or entirely within homogeneous regions, but do not cross the interface. This means that it is advantageous to place the vertices of the triangles (nodes) on the interfaces between materials.
Fundamental difficulties that becomes apparent to users of ppm2oof's adaptive meshing scheme are:
-
Because no node can be left hanging (a hanging node is one that is attached to the corner of one triangle but does not attach to the corners of the adjacent triangles), the element size must change gradually from regions of coarse to fine mesh.
-
Because the pixel/property regions are set on a square grid, the interfaces will be "stair-stepped". Attempts to resolve the interface with edges that are not constrained to the square grid will sometimes leave small strange-looking triangles at the interfaces. [28] If they are small enough, they will probably not have much effect on linear computations, but they certainly distract from the aesthetic qualities of the image. They can also adversely affect element-by-element quantities, such as stress distributions.
Creating a nice mesh is not difficult, but there is a modicum of art and persistence involved. It is useful to save your work in a log-file, or stack your meshes in the mesh stack and be willing to make mistakes and trash them. [29]
Most artful meshers agree that it is wise to jump between moving nodes, refining triangles, swapping, moving, etc. There is no agreement on just how to do it--you have to learn through practice and careful observation. Needless to say, we hope that this visual method of mesh creation is easier than doing it by hand.
As a first attempt, it is useful to create a fairly coarse mesh that will adaptively iterate quickly. Picking the initial mesh parameters that will land all the nodes at the edge of pixels is also useful. Try to move, by mousing, the few most obvious nodes to visible boundaries between material types. Run the automatic node motion functions--first with large steps and then with smaller ones. Do a mesh refine and compare the element (triangles) display to the pixel property display. Cycle through the steps--manual motion of any obvious pixels to boundaries, automatic node motion, triangle swapping, refining--until you are reasonably satisfied.
Your intuition for making meshing decisions will be improved if you have some understanding of the meshing algorithm.
The mesh is adapted by creating a cost (or mesh-energy) function that will be minimized as the mesh becomes optimized. The mesh is optimized by combinations of refining triangles (creating elements within existing elements) and moving nodes.
The mesh-energy function is a weighted linear combination two independent energy functions--one to make the mesh uniform (Eshape) and the other to make the elements homogeneous (Ehomog). The linear combination,
is what ppm2oof will try to minimize. The parameter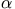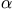
is a variable that can be specified in this
menu.
For each element,
where A is the element area and L is the element perimeter. Eshape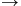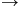
0 for an equilateral triangle and Eshape
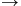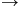1 for a tall skinny triangle or a short fat one.
Each element adds its own Eshape to a sum--that is
multiplied by (1 - 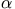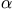)--that becomes the shape
part of the mesh-energy function.
Each element may cover whole and fractional pixels-- the most useful elements will cover pixels of only one type. For these purposes, two pixels have a different type if they have different materials, different material parameters, or belong to different groups. For each element,
where ai is the area of the ith material type within the element, A is the area of the element, and N is the total number of different pixel types in the mesh. [30] This is a positive function with a global minimum value of zero if the element is homogeneous. Each element contributes to a sum--multiplied by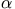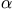
--that
is added to the shape sum. When computing
ai, ppm2oof takes into account the
fact that a pixel may lie in more than one element, and
computes the fractional area in the element.
The mesh-energy function is non-linear and optimization is not straightforward. Optimization can get stalled by local minima in the mesh-energy and is also fraught with difficulties imposed by the discrete pixel grid underlying the computation. Optimization by node motion through mesh-energy gradient descent is available, but is slow--and frankly a bit cranky. Monte Carlo methods (annealing) seem to work quite well.
[27] The term "adaptive meshing" is used in other contexts to mean the modification of a finite element mesh during the solution process. This is not what ppm2oof does. ppm2oof adapts the mesh to the complex microstructural geometry, which is only a first step towards adapting it to the solution of a physics problem on that geometry.
[28] At the time of this writing, no methods for element deletion exist in ppm2oof.
[29] However, you can quickly make the mistake of over meshing and crashing the program when it runs out of memory. This can be minimized be reducing the mesh stack. Nevertheless, if you think you can get away with setting the number of refine iterations to a large number, you've thunk wrong, thank you.
[30] Ehomog is identically zero if N=1.
